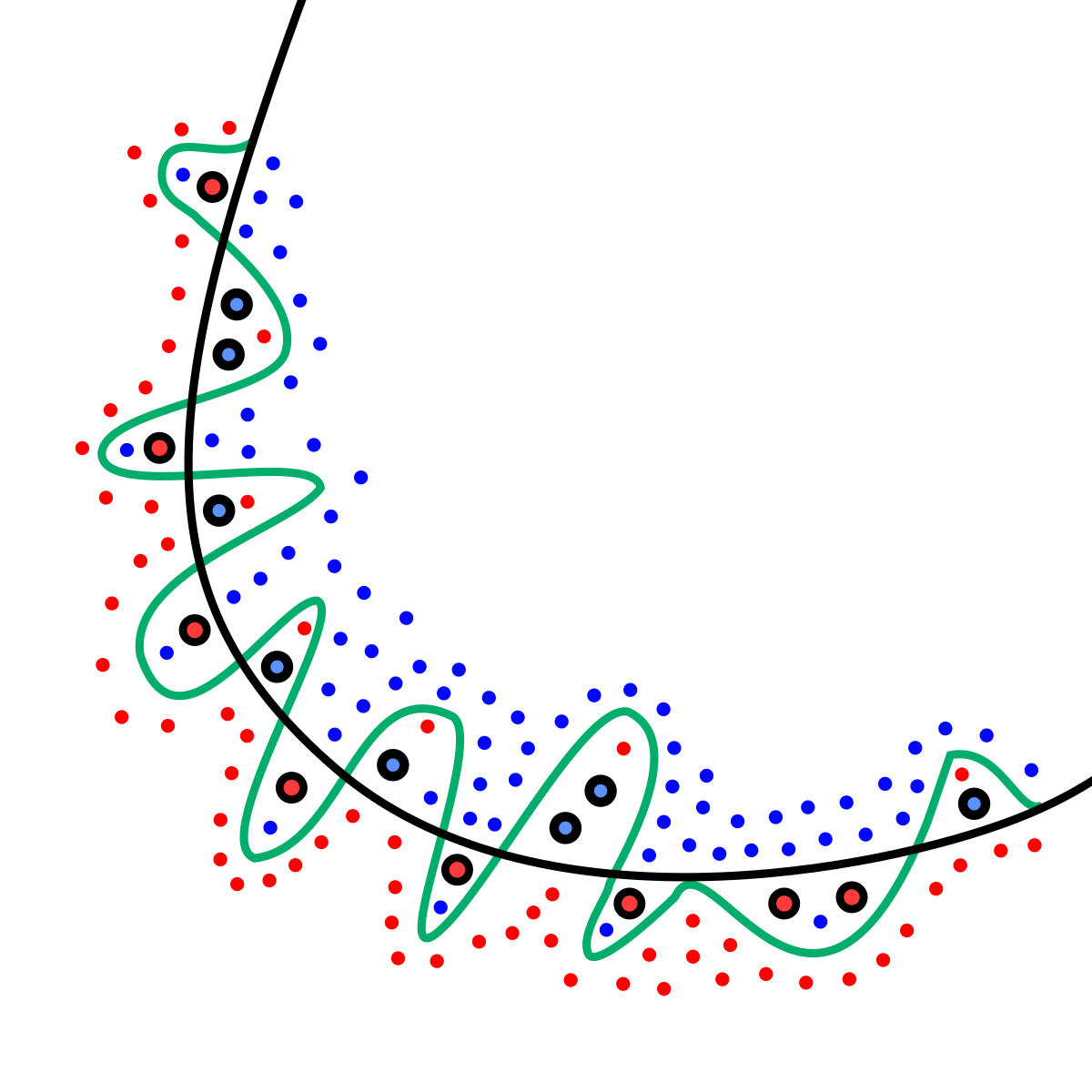
Overfitting is a phenomenon in which the model is trained too well over a specified data that it fails to recognize patterns outside the training set.

This can be optimized using different methods like:

• Weighted Regularization(L1 and L2)
• Activity Regularization
• Weight constraint
• Dropout
• Noise
• Stopping the training process by evaluating the performance.

We will focus on L1 and L2 regularization for now.
L1 and L2 functions are Loss Functions which are usually used in Weighted Regularization method to minimize error.

L1 Loss Function:

L1 loss function is also known as Least Absolute Deviations(LAD). A linear regression model that uses L1 for regularization is called lasso regression. The linear regression model's equation/model will not change in both of these methods. The output y(Here, Ytrue) is supposed to be the ideal value predicted and yhat(Here, Ypredicted) is the output value predicted after the computation using their respective activation functions. This involves the modulus of difference of y and yhat iterated on all training examples. This is usually preferred on training examples that contain outliers for training and further regularisation. One advantage is that L1 loss has the ability to push some features(x) to zero reducing model complexity.

L2 Loss function:

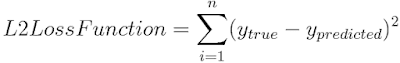
L2 loss function is also known as Least Squared Errors(LSE). A linear regression model that uses L2 for regularization is called ridge regression. The linear regression model's equation/model will not change in both of these methods. The output y(Here, Ytrue) is supposed to be the ideal value predicted and yhat(Here, Ypredicted) is the output value predicted after the computation using their respective activation functions. This involves the square of difference of y and yhat iterated on all training examples. L2 has the ability to shrink the coefficient of features throughout the training set which is quite helpful in approaching problems that require collinear or codependent values.

Note: The fact that L1 loss converges features to zero is not limited to the latter only.