Coalitional Game Theory
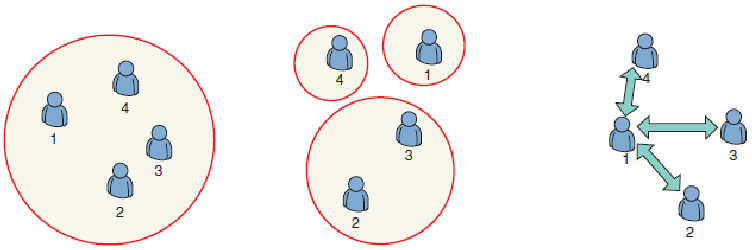
In game theory, a coalitional game is a kind of situation where a group of people works under the same strategy to achieve the common goal, unlike non-cooperative game theory where individuals compete with each other in order to maximize payoff. It is also known as cooperative game theory.
We experience a lot of situations where this conditional game can be observed. Whether it is as small as splitting the restaurant bills among friends or it is as large as an alliance between two nations.
Unlike a normal game which focuses on individual, cooperative game focus on groups of agents. It tells how will each group of agents work. It is important to know that it does not tell how the agents make individual choices with the coalition and how they coordinate among themselves in the group.
Utility function in game theory do the following for each individual player-
- It measure the degree of preference
- It shows the situation of uncertainty
- Is an act of maximizing the expected utility by each player.
The utility for this type of game which is called transferable utility. which means whatever utility is achieved by the group it is possible to distribute it among the group as per the contribution.
Under this assumption here's how we can define a coalitional game.
A coalitional game with the transferable utility is a pair (N,v), where
- N defines the number of player participating in the game and are indexed by i.
- v is utility function for coalitional games. It says for every possible subset of the players S, which include up to or equal to all the members what is the utility group can achieve and how to divide among its members.
How the coalition is formed?
Most of the time answer to this is a grand coalition where all the agents agree to work together. However, in order to confirm this sometimes, we need to look at how the payoff is divided among the individuals. This will help us in understanding it better.
We can call a coalitional game is superadditive if for all pairs of coalitions let's suppose S and T which are both strict subsets of N and if the intersection between these 2 coalitions is empty, which means these two coalitions involve an entirely different set of players. Then, if we make a new coalition, S union T, that combines these 2 coalitions together then the value of this larger coalition is at least as big as the sum of the values of the 2 coalitions alone. So, in layman language. if we make a bigger coalition out of two independent coalitions, then the value of that bigger coalition is always at least as big as the sum of the values that those two independent coalitions.
Superadditivity is justified when a coalition can always work without interfering with one another. The value of two coalitions will be no less than the sum of an individual coalition which tells that a grand coalition has the highest payoff.
How utility is divided among the group
Another main question is how much each player has contributed to the group and the utility is divided among the group. Coalitional games have something called Shapley value. It’s a method of dividing gain or profit among the group on the basis of how much they have contributed which is defined by several axioms-
- The contribution of each player is determined by what is gained or lost by removing that player from the group. This is called the marginal contribution.
- i and j suppose two players are interchangeable relative for the group if they always contribute the same amount to every coalition. This is called symmetry. Interchangeable players get same utility.
- A player is a dummy player is it contributes nothing and ideally paid nothing.
- If a game has multiple parts, cost or payment should be decomposed across those parts.
The mathematical formula of Shapley value can be given by this-
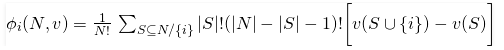
It is calculated by considering all the possible orders of the arrival of the players into the situation and giving each player his marginal contribution. We're not going to go through the complex formula in detail but we'll go through explanation using an example.
Let us go through a simple example for the coalitional game.
Suppose that there are two person Sam and John.Sam alone can make and sell 10 pots in a day and John makes and sell 15 pots in a day .One day they decided to work together and ended selling 30 pots together.Now how the utility is divided among the two ?
Now,
- Sam’s when working alone is v({Sam}) = 10;
when John arrives the amount increases to v({Sam,John}) = 30
therefore John’s marginal contribution is v({Sam,John}) - v({Sam}) = 30 - 10 = 20. - John’s when working alone is v({John}) = 15;
when Sam arrives the amount increases to v({Sam,John}) = 30
therefore Sam’s marginal contribution is v({Sam,John}) - v({John}) = 30 - 15 = 15.
Thus we have the following table:
| Probability | Situations | Sam's Marginal Contribution | John's Marginal Contribution |
|---|---|---|---|
| 0.5 | Sam working alone then John joined him | 10 | 20 |
| 0.5 | John working alone then Sam joined him | 15 | 15 |
Thus
Sam’s expected marginal contribution is: 1/2*10 + 1/2*15 = 12.5
John’s expected marginal contribution is 1/2*20 + 1/2* 15 = 17.5.
This is the Shapley value: x1= 12.5 and x2= 17.5
So, above all are some basic concepts for the coalitional game. Try to get more in-depth about the topic by reading "Theory of Games and Economic Behavior" by John von Neumann and Oskar Morgenstern.
